A Short Round-Up of Topology-Based Papers at ICLR 2021
Tags: research
With ICLR 2021 having finished a while ago, I wanted to continue series. See here and here for summaries of previous conferences. This time, I will present three papers that caught my eye—they are all making use of topological concepts to some extent.
Caveat lector: I might have missed some promising papers. Any suggestions for additions are more than welcome! Please reach out to me via Twitter or e-mail.
Hu et al.: Topology-Aware Segmentation Using Discrete Morse Theory
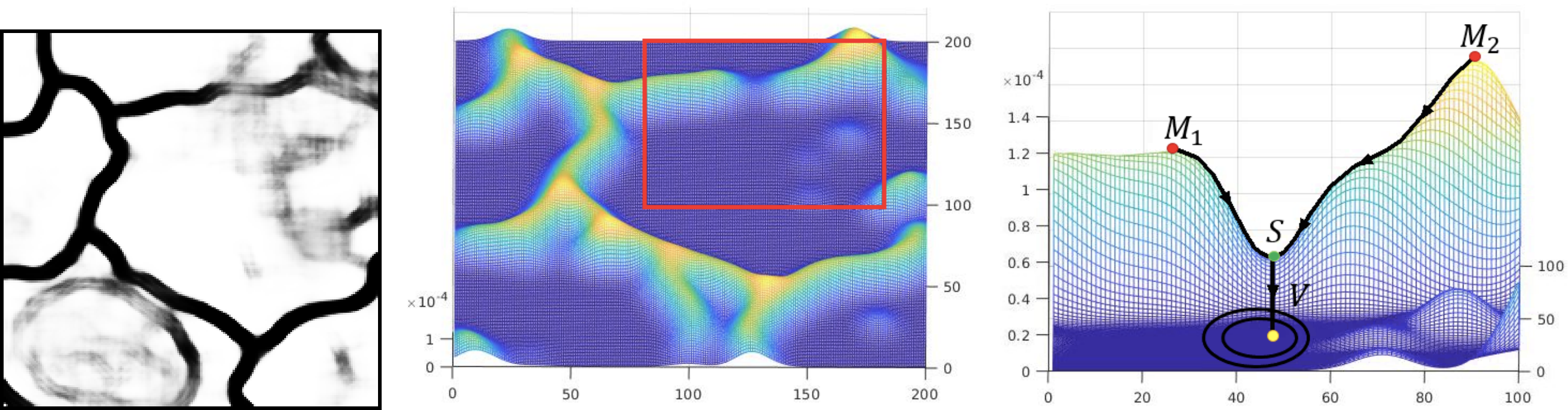
Topology-Aware Segmentation Using Discrete Morse Theory by Xiaoling Hu, Yusu Wang, Li Fuxin, Dimitris Samaras, and Chao Chen demonstrates how to employ topological concepts in order to improve segmentation techniques. This is achieved by ensuring that the Betti numbers—essentially, counts of topological features—are maintained by a segmentation. The paper is part of a strand of research that develops topology-based loss terms in order to regularise the output of a model.1 Another interesting aspect of this paper is that introduces concepts from Morse theory to the community. This, in my opinion, is long overdue—Morse theory offers such a great perspective in explaining the loss landscape, for instance.
I am also happy to see how topological methods are now sufficiently mature to be serious alternatives to other methods. The application area of image segmentation is therefore a perfect fit to demonstrate the capabilities of additional connectivity constraints; it sidesteps a lot of the issues that usually arise when we try to allude to the utility of topological features in high-dimensional spaces.
Kyriakis et al.: Learning Hyperbolic Representations of Topological Features

Learning Hyperbolic Representations of Topological Features by Panagiotis Kyriakis, Iordanis Fostiropoulos, and Paul Bogdan deals with an ever-present problem, viz. the representation of topological features. Practitioners already know that the common persistence diagram or persistence barcode representations are fraught with certain shortcomings, such as the computational complexity of their comparison or how to deal with features of infinite persistence.2
The approach by Kyriakis et al. solves this issue by an ingenious trick: they learn a hyperbolic representation, in which features of infinite persistence are put close to the boundary of the respective representation. This neatly corresponds to such features approaching an infinite distance to other features of finite persistence. The approach itself is simple, which I appreciate, involving merely a certain parametrisation of maps into hyperbolic space. I have not seen applications of this approach ‘in the wild’ yet, but I reckon that this might make a good addition to everyone’s toolbox.
On a more abstract level, this paper exemplifies the growing interest of the ML community for ’non-standard’ spaces. If such endeavours continue to prove successful, maybe the established paradigm of ‘Euclidean spaces should be enough for everybody’ will be toppled.
Zhou et al.: Evaluating the Disentanglement of Deep Generative Models through Manifold Topology

Last, but certainly not least, I want to briefly present Evaluating the Disentanglement of Deep Generative Models through Manifold Topology by Sharon Zhou, Eric Zelikman, Fred Lu Andrew Ng, Gunnar Carlsson, and Stefano Ermon. This paper is bound to catch many more eyes, because the author list is highly notable, containing Gunnar Carlsson, one of the founders of TDA, and Andrew Ng, one of the ’evangelists’ of modern ML. Maybe this will put TDA on the radar of more ML researchers.
In any case, the paper discusses a timely topic, viz. the quantification of disentanglement of models. Briefly put, disentangled representations refer to learned representations in which individual latent variables correspond to separate factors of a model. The classical example is that a model containing rotations and scale changes should ideally be described in a factorised representation by two ‘orthogonal’ factors, making it possible to control either one of these aspects individually. The paper now builds on the previous ICML publication Geometry Score: A Method For Comparing Generative Adversarial Networks, which presents a general method for comparing the topology of distributions. The paper by Zhou et al. now measures topological (dis)similarity across the latent dimensions of the manifold, such that all submanifolds may be clustered according to it.
I am excited about such a method because it presents a compelling case for the utility of topological features. Future work in this area should try to move from the purely observational to the interventional,3 though, and enforce such disentanglement automatically via topology.
Summary
Another year, another conference, another set of papers. As our Workshop on Geometrical and Topological Representation Learning at ICLR 2021 demonstrated, there’s a growing interest in such methods, and interest in TDA is growing. I am very glad to see that our methods even found a receptive audience at ICLR, arguably one of the conferences that has a penchant for ‘deep learning’ approaches first and foremost.4 We still have numerous challenges to tackle for the future, but I remain an eternal optimist and am confident that we will make progress!
-
Another example of this concept is our paper Topological Autoencoders, presented at ICML 2020. ↩︎
-
These features are often also dubbed ’essential,’ but care must be taken not to misinterpret this. They are only essential because of the choice of simplicial complex, typically. ↩︎
-
This is a categorisation we introduced in our recent survey on topological machine learning. ↩︎
-
This is the whole reason why the conference was founded in the first place. I am not criticising its focus, just expressing my pleasant surprise about the fact that it accepts TDA papers. ↩︎