Tags: research

« Previous post: Why your academic code needs a software … — Next post: Minimum elucidating examples »

With this year’s International Conference on Machine Learning (ICML) being over, it is time to have another instalment of this series. Similar to last year’s post, I shall cover several papers that caught my attention because of their use of topological concepts—however, unlike last year, I shall not restrict the selection to papers using topological data analysis (TDA).

Caveat lector: I might have missed some promising papers. Any suggestions for additions are more than welcome! Please reach out to me via Twitter or e-mail.

Chen et al.: Learning Flat Latent Manifolds with VAEs

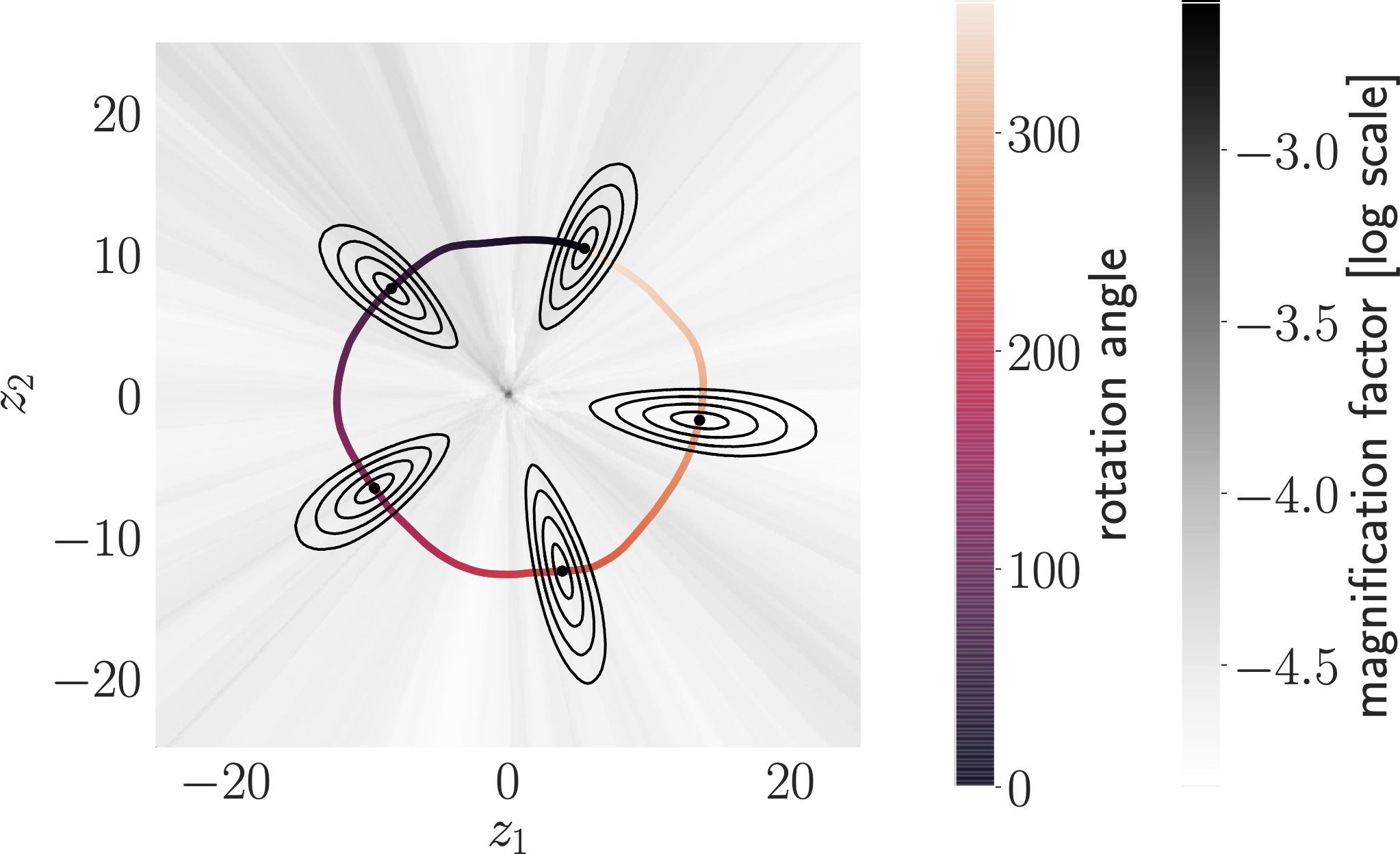
Learning Flat Latent Manifolds with VAEs by Nutan Chen, Alexej Klushyn, Francesco Ferroni, Justin Bayer, and Patrick van der Smagt discusses an interesting modification of variational autoencoders, viz. an extended loss term that regularises the latent space to be flat (i.e. having no curvature). The main idea is to ensure that the Riemannian metric tensor is the identity matrix.

The ingenious implication of such a latent space is that the Euclidean distance is a good proxy for the similarity between data points, whereas this is not a priori the case for other latent spaces. It is interesting to note that there is a ‘sibling’ paper to this one, which was published at ICLR 2020, namely Mixed-curvature Variational Autoencoders. This paper presents an autoencoder whose latent space is a product of Riemannian manifolds, whose curvature is either fixed or learnable.

I am glad to see that curvature is starting to attract more attention from the machine learning community. It is such a fundamental property of a manifold but can influence the validity of many calculations in latent spaces. It also has some beneficial properties for graph classification, but this is maybe a better topic for a subsequent post!

Hofer et al.: Graph Filtration Learning

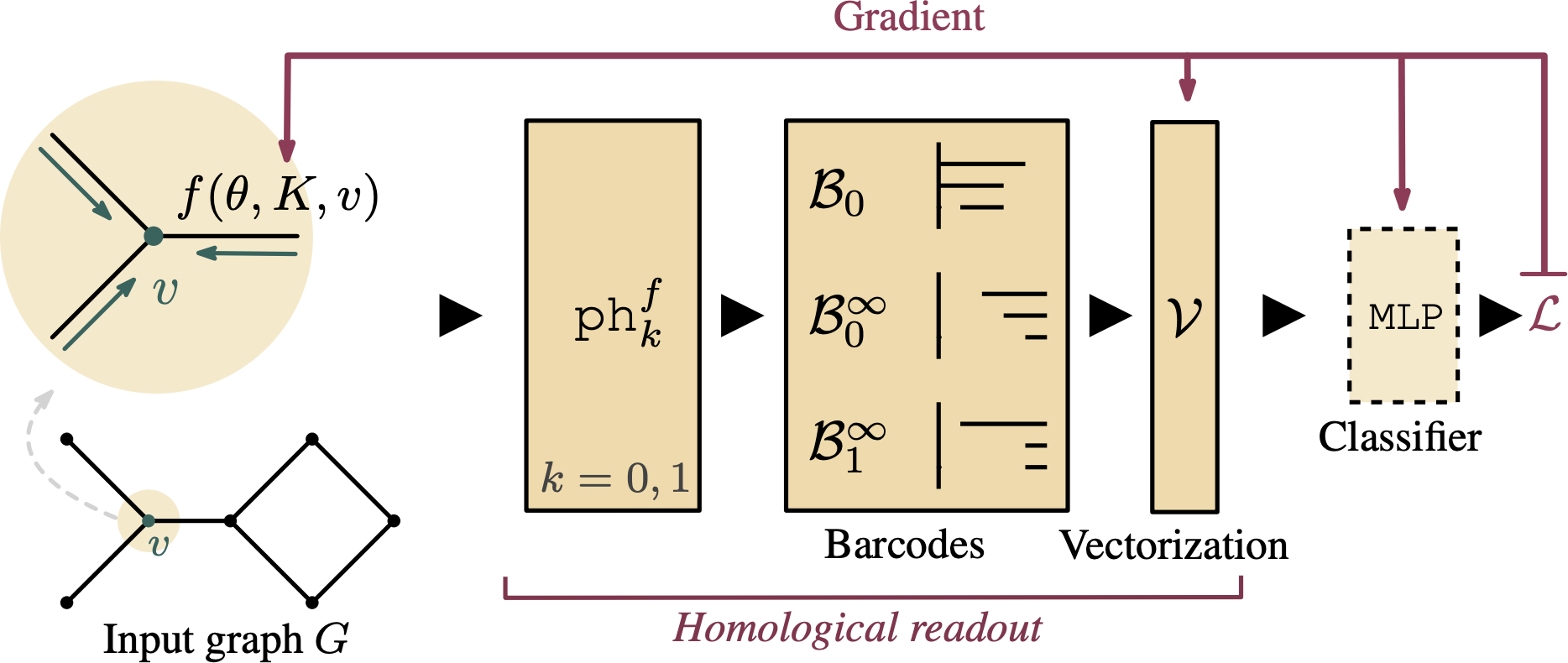
Graph Filtration Learning by Christoph Hofer, Florian Graf, Bastian Rieck, Marc Niethammer, and Roland Kwitt is arguably¹ the first step towards properly integrating topological features into neural networks for graph classification! Briefly put, we developed a homological READOUT function (to use the parlance of graph neural networks) that gives rise to a learnable filter function—a filtration.

This concept might be unknown to some readers, but a filtration in this context is a scalar-valued function on the vertices of a graph that permits sorting it. Filtrations serve as the backbone for many topology-based algorithms, primarily for the aforementioned persistent homology, which permits us to study multi-scale topological features (connected components, cycles, etc.) of an object. Prior to this paper, filtrations were pre-defined or chosen based on some target function, such as the vertex degree function of a graph. Our approach changes this—leading to a filtration that is learnable in an end-to-end fashion and thus specifically designed for a classification problem.

We manage to achieve this by first initialising our filter function based on a regular graph neural network; essentially, one level of message passing between nodes is sufficient. This provides us with a non-trivial filter function whose performance we can subsequently adjust by calculating the topological features induced by said filter, and vectorising the resulting representations. Since each of these steps is differentiable², the resulting function is also differentiable, making it possible to adjust the filter for the best classification results.

I would recommend this paper to anyone who is interested in learning more about the benefits that a topology-based perspective brings to certain application problems. Being able to learn the right topological features to classify a set of graphs opens up exciting opportunities.

Hofer et al.: Topologically Densified Distributions

Topologically Densified Distributions by Christoph Hofer, Florian Graf, Marc Niethammer, and Roland Kwitt studies regularisation properties of over-parametrised neural networks in the context of small sample-size learning. This is achieved by studying the properties of latent representations (the paper uses the term internal representation, but this is equivalent). More precisely, generalisation properties are analysed via the push-forward probability measure induced by the latent representation (or encoding).

The authors show that probability mass concentration around training samples in the latent space is linked to the generalisation capabilities of a model, but, even more exciting, such a concentration can be achieved by applying topological constraints on samples from that space! In the context of this paper, such constraints pertain to measuring the connectivity of samples. This is achieved using persistent homology, specifically, by calculating a zero-dimensional Vietoris–Rips complex—if you are not familiar with this term, just think of a minimum spanning tree.

What I particularly enjoyed about this paper is that it starts providing solid answers to fundamental concepts in machine learning. All too often, we remain in the realm of the empirical and just observe whether our network generalises. This paper ventures into hitherto-unknown territories and gives us a theoretical justification!

Moor et al.: Topological Autoencoders

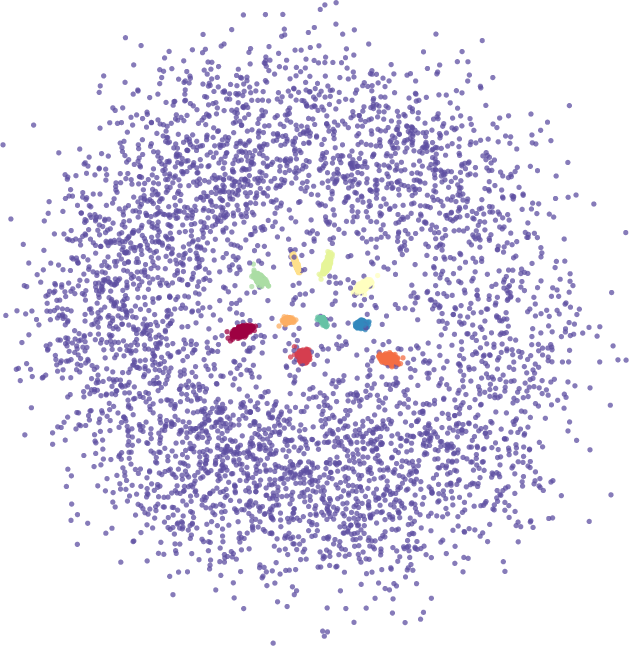
Topological Autoencoders by Michael Moor, Max Horn, Bastian Rieck, and Karsten Borgwardt deals with regularising the latent space in terms of its topology. More precisely, we preserve the topological features of the input data in the respective latent space (on the batch level, respectively). While we restrict our experiments to connected components for now (so no cycles yet, even though our method generalises to higher dimensions), our approach makes it possible to create latent representations that ‘mimic’ the topological features of the input.

This leads to a nice plug-and-play loss term that can be easily integrated into most architectures, and we can demonstrate that, among others, it considerably improves the quality of a ‘vanilla’ autoencoder architecture. To achieve this goal, we had to solve all kinds of interesting adventures, one of them being how to make everything differentiable. Interestingly, we end up with a similar necessary condition for differentiability than for the graph filtration learning paper, viz. the pairwise distances between different samples of the input batch need to be unique.

The coolest feature of our method is that it technically only requires a distance metric between input samples³, nothing more—no feature vector representation or anything. It can thus conceivably be used to represent the topology of any object you fancy (including documents, images, and graphs).

If you are interested in a beautifully-animated high-level introduction to this publication, you should take the time to read Michael’s blog post on our paper.

Rezende et al.: Normalizing Flows on Tori and Spheres

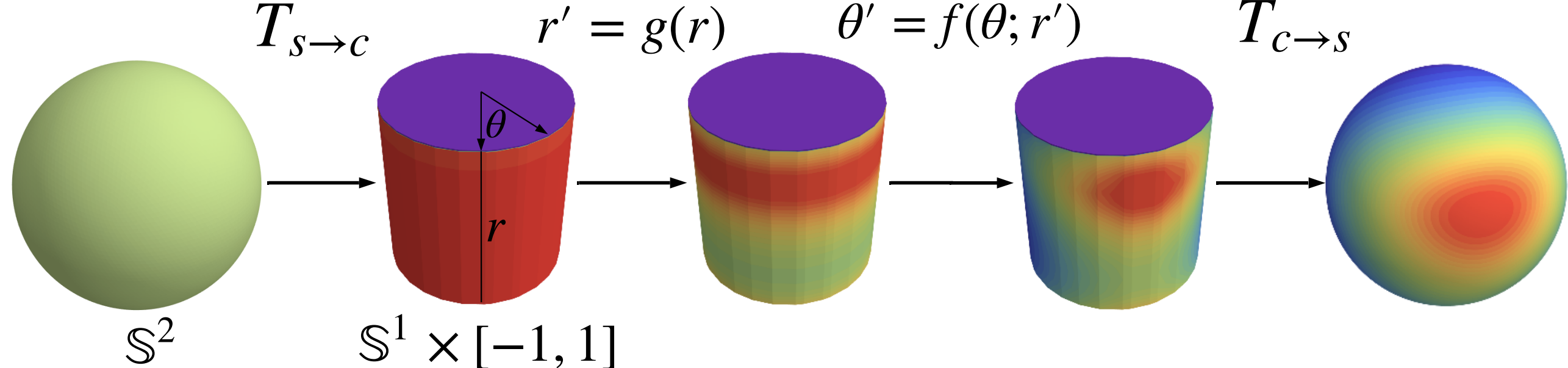
Normalizing Flows on Tori and Spheres by Danilo Jimenez Rezende, George Papamakarios, Sébastien Racanière, Michael S. Albergo, Gurtej Kanwar, Phiala E. Shanahan, and Kyle Cranmer present a novel method for calculating normalising flows on more complex spaces than the usual Euclidean ones. Specifically, as the title implies, they develop methods for calculating such flows on tori and spheres.

What I enjoyed about this paper is the smart way of constructing flows iteratively: first, flows on the circle are being constructed (using different concepts for defining a diffeomorphism, the most favourite of mine being a Möbius transformation). Since a torus can be described as the Cartesian product of circles, this is sufficient to describe flows on tori of arbitrary dimensions! Next, the flows are generalised to higher-dimensional spheres.

While I am by no means and expert in normalising flows, I liked reading this paper a lot. The theory is well-developed and it is another one of those publications that shows you how to go beyond the boundaries of what is currently possible. Moreover, I enjoyed the discussion of the implementation details—it turns out that achieving numerical stability here is another feat that deserves some mention!

Summary

This year’s ICML also featured an interesting array of topology-based papers. Not all of them fit neatly into the field of topological data analysis (TDA), but I am happy to see that the community is starting to pick up this fundamental topic. I remain convinced that a topology-driven perspective is needed to answer certain foundational questions in machine learning. Here’s to the future of topology!