A round-up of topological data analysis papers at ICML 2019
Tags: research
Even though this year’s International Conference on Machine Learning (ICML) is not quite over yet, I wanted to put down some thoughts about the many inspiring papers I encountered here. Specifically, I will briefly introduce all papers that deal with methods from topological data analysis (TDA) as this is one of the topics of my research.
Caveat lector: I might have missed some promising papers. Any suggestions for additions are more than welcome. Please reach out to me via Twitter or e-mail.
Hofer et al.: Connectivity-Optimized Representation Learning via Persistent Homology
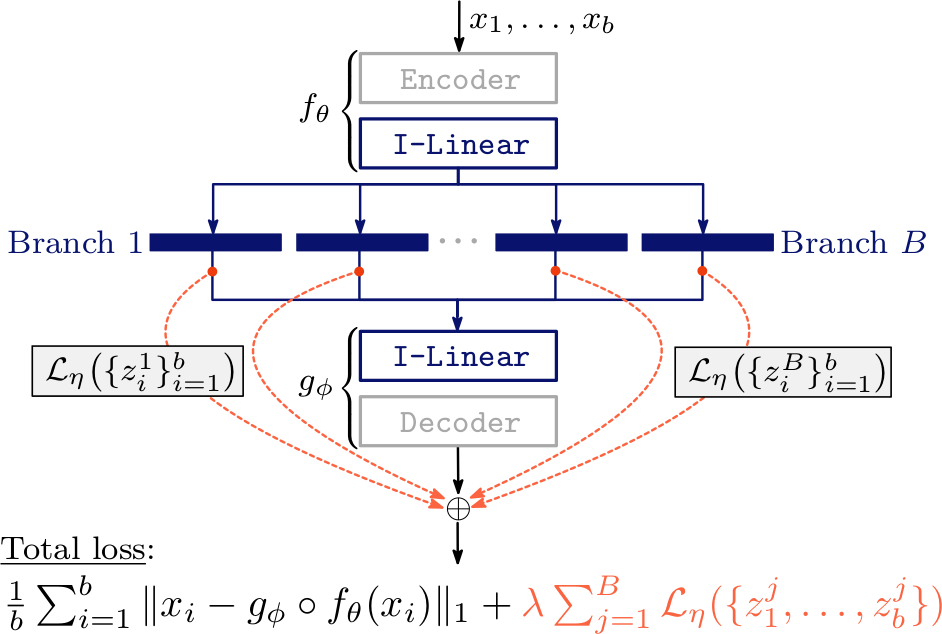
Connectivity-Optimized Representation Learning via Persistent Homology by Christoph Hofer, Roland Kwitt, Marc Niethammer, and Mandar Dixit deals with controlling the latent space of an autoencoder by imposing additional connectivity restrictions. This is achieved by calculating topological features using persistent homology. The paper describes a novel connectivity loss term that is differentiable, thereby very elegantly removing the biggest obstacle that prevented persistent homology being used in a continuous setting. Finally, backpropagation through the persistent homology calculation is possible!
Similar ideas along these lines (but placed in different contexts) can be found in A Topological Regularizer for Classifiers via Persistent Homology and Topological Function Optimization for Continuous Shape Matching.
Kunin et al.: Loss Landscapes of Regularized Linear Autoencoders
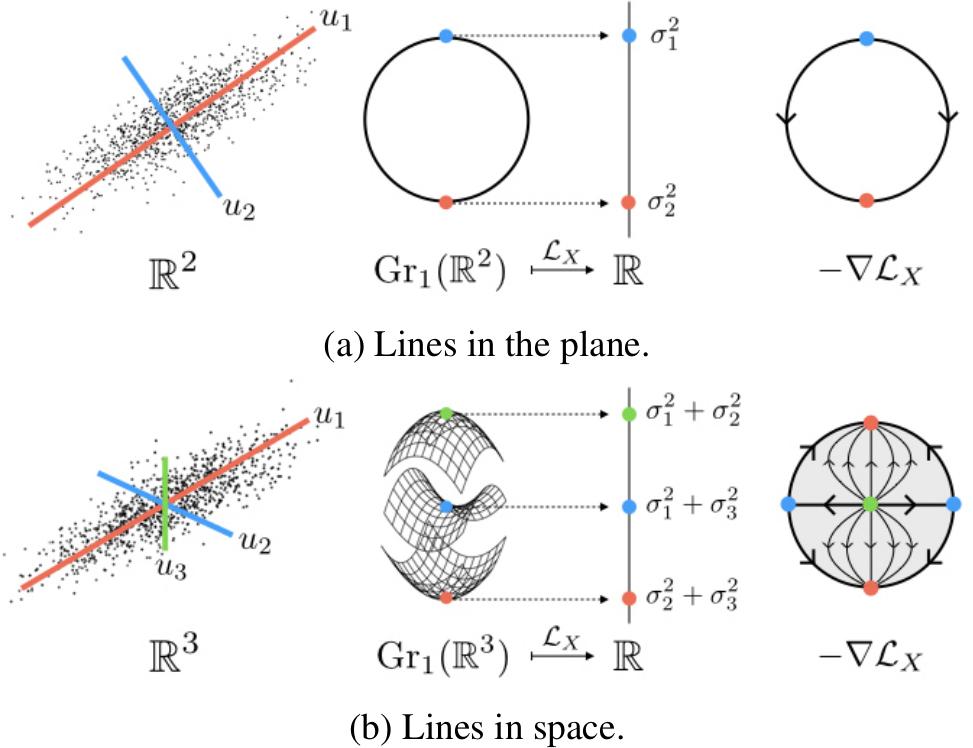
In their paper Loss Landscapes of Regularized Linear Autoencoders, Daniel Kunin, Jonathan Bloom, Aleksandrina Goeva, and Cotton Seed analyse the loss landscape of a specific class of autoencoders. Their paper is extremely readable and interesting but the real kicker (for me) is that they use Morse theory to prove properties of the loss function! Moreover, their proofs are very accessible and instructive—the supplementary materials of this paper provide one of the best panoramic overviews of a big chunk of algebraic topology that I am currently aware of.
Mémoli et al.: The Wasserstein Transform
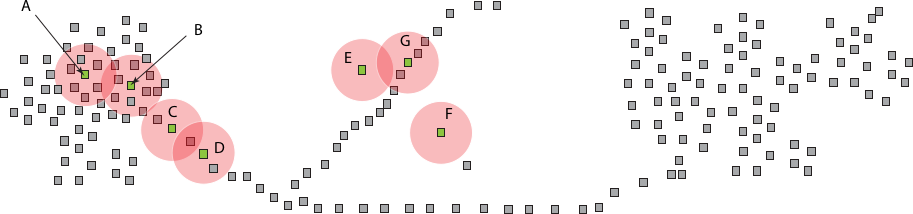
In The Wasserstein Transform, Facundo Mémoli, Zane Smith, and Zhengchao Wan present a general transformation for data sets (or metric spaces, to be more precise) that performs a denoising operation based on optimal transport theory. Connections to the venerable mean shift algorithm are also drawn.
While not directly employing TDA techniques, this paper makes the very interesting case that its transformation could be used to potentially strengthen the ’topological signal’ that is underlying a data set. I feel reminded of Topological De-Noising: Strengthening the Topological Signal by Jennifer Kloke and Gunnar Carlsson, in which a modified variant of mean shift is used (not based on optimal transport theory, though) to perform thresholding.
Nguyen: On Connected Sublevel Sets in Deep Learning
In his paper On Connected Sublevel Sets in Deep Learning, Quynh Nguyen analyses sublevel sets of the loss function. While not directly employing TDA techniques, sublevel sets are of course an integral part of TDA and crop up all over the place—see my article on Morse theory, for example. The paper proves that sublevel sets of a certain class of deep networks are connected and unbounded. This, in turn, implies that no ‘bad’ (in terms of training performance) local valleys exist in the loss landscape. A very interesting theoretical paper that I definitely want to read in much, much detail.
A loosely related paper from this year’s ICLR is Deep, skinny neural networks are not universal approximators by Jesse Johnson that employs a characterisation of level sets of neural networks to disprove the universal approximator property.
Ramamurthy et al.: Topological Data Analysis of Decision Boundaries with Application to Model Selection

The paper Topological Data Analysis of Decision Boundaries with Application to Model Selection presents a very nice approximation of the decision boundary of a classifier by means of a labelled Vietoris–Rips complex (and a corresponding Čech complex). Using this approximation, the complexity of the decision boundary can be modelled. This, in turn, facilitates model selection from a ‘marketplace’: the model that most closely matches the topological features of the decision boundary can be picked.
This is very exciting because it is one of the first papers to work with a topological approximation of the decision boundary of a network. There are some preprints, such as the work by Guss and Salakhutdinov, that deals with a similar setting. Plus, there is of course our own work, also from this year’s ICLR, that deals with assessing the complexity of a neural network, albeit in terms of the weight space itself and not the decision boundary.
Rieck et al: A Persistent Weisfeiler–Lehman Procedure for Graph Classification

In A Persistent Weisfeiler–Lehman Procedure for Graph Classification, we (that is, Christian Bock, Karsten Borwardt, and myself) propose a novel way to integrate topological features into the Weisfeiler–Lehman graph kernel framework. We manage this by defining a metric on the aggregated multisets of each node neighbourhood. In turn, this makes it possible for us to define a filtration on the graph. The persistent homology of that filtration, together with the hashed graph labels, permits us to derive a set of feature vectors that incorporate both topological information (in the form of connected components and cycles), as well as label information.
Summary
I am happy and excited about seeing that TDA and its related methods are thriving and starting to carve out their space in machine learning. Let’s see what the future holds! I sincerely hope that this will not be the last post of this sort.